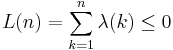Pólya conjecture
In number theory, the Pólya conjecture stated that 'most' (i.e. more than 50%) of the natural numbers less than any given number have an odd number of prime factors. The conjecture was posited by the Hungarian mathematician George Pólya in 1919,[1] and proved false in 1958. The size of the smallest counter-example is often used to show how a conjecture can be true for many numbers, and still be false.
Contents |
Statement
Pólya's conjecture states that for any n (> 1), if we partition the natural numbers less than or equal to n (excluding 0) into those with an odd number of prime factors, and those with an even number of prime factors, then the former set has at least as many members as the latter set. (Repeated prime factors are counted the requisite number of times—thus 24 = 23 × 31 has 3 + 1 = 4 factors i.e. an even number of factors, while 30 = 2 × 3 × 5 has 3 factors, i.e. an odd number of factors.)
Equivalently, it can be stated in terms of the summatory Liouville function, the conjecture being that
for all n > 1. Here, λ(k) = (−1)Ω(k) is positive if the number of prime factors of the integer k is even, and is negative if it is odd. The big Omega function counts the total number of prime factors of an integer.
Disproof
Pólya's conjecture was disproven by C. B. Haselgrove in 1958. He showed that the conjecture has a counterexample, which he estimated to be around 1.845 × 10361.[2]
An explicit counterexample, of n = 906,180,359 was given by R. Sherman Lehman in 1960;[3] the smallest counterexample is n = 906,150,257, found by Minoru Tanaka in 1980.[4]
The Pólya conjecture fails to hold for most values of n in the region of 906,150,257 ≤ n ≤ 906,488,079. In this region, the Liouville function reaches a maximum value of 829 at n = 906,316,571.
Notes
- ^ Pólya, G. (1919). "Verschiedene Bemerkungen zur Zahlentheorie". Jahresbericht der deutschen Math.-Vereinigung 28: 31–40. JFM 47.0882.06.
- ^ Haselgrove, C.B. (1958). "A disproof of a conjecture of Pólya". Mathematika 5 (02): 141–145. doi:10.1112/S0025579300001480. MR0104638.
- ^ Lehman, R. S. (1960). "On Liouville's function". Mathematics of Computation (Mathematics of Computation, Vol. 14, No. 72) 14 (72): 311–320. doi:10.2307/2003890. JSTOR 2003890. MR0120198.
- ^ Tanaka, M. (1980). "A Numerical Investigation on Cumulative Sum of the Liouville Function". Tokyo Journal of Mathematics 3 (1): 187–189. doi:10.3836/tjm/1270216093. MR0584557.
References
- Weisstein, Eric W., "Pólya Conjecture" from MathWorld.